
Reinforcement Bar Cutoffs and Bend Points
Generally, it is followed to cut or bend primary reinforcement in beams and slabs where it is not necessary. But tensile steel can?t be suspended perfectly at the theoretical cutoff or bend points. It is essential to withstand tensile forces in the reinforcement via embedment outside those points.
All reinforcement will expand outside the point at which it unnecessary to stand flexure for a distance equivalent to the actual depth of the member or 12 bar diameters, whichever is higher excluding at supports of simple spans and at free end of a cantilever. A simple span provides support to use the smaller extensions and at the free end of a cantilever.
Continuing reinforcement must contain an embedment length outside the point where bent or terminated reinforcement is unnecessary to withstand flexure. Similar to development length ld, the embedment should be as long as a minimum.
Flexural reinforcement must not be in a tension zone unless one of the following conditions is satisfied:
1. Shear is below two-thirds that generally allowable along with allowance for shear reinforcement, if any.
2. Continuing bars offer double the area essential for flexure at the cutoff, and the shear is under three-quarters of that allowable (No. 11 bar or smaller).
3. Stirrups more than those generally essential which are provided each way from the cutoff for a distance identical to 75% of the effective depth of the member. Area and spacing of the additional stirrups should be as 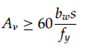
Where, Av denotes stirrup cross-sectional area, in2
bw denotes web width, in
S denotes stirrup spacing, in
fy denotes yield strength of stirrup steel, psi
Stirrup spacing will be under 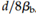 ,
, 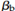 where denotes the ratio of the area of bars cut off to the whole area of tension bars at the section and d denotes the effective depth of the member.
where denotes the ratio of the area of bars cut off to the whole area of tension bars at the section and d denotes the effective depth of the member.
The position of theoretical cutoffs or bend points is generally obtained from bending moments as the steel stresses are nearly symmetrical to them. The bars usually are suspended in groups or pairs. As for instance, while bending the bars, the theoretical bend-up point is located at the section where the bending moment is two-thirds the maximum moment. The point is available as analytically or graphically.
Ref: theconstructor.org

