Derivation of D^2/162 and D^2/533 for unit weight of steel calculation
The quantity surveyor frequently applies two vital formulas like D^2/162 and D^2/533 for measuring the weight of steel.
In the following youtube tutorial you will get the detail information on these vital formulas as well as how these formulas are derived.
This tutorial will help you to find out the weight of steel for several structural materials in kilograms.
If the length of the steel is known, the weight of steel per unit length can be measured with these formulas.
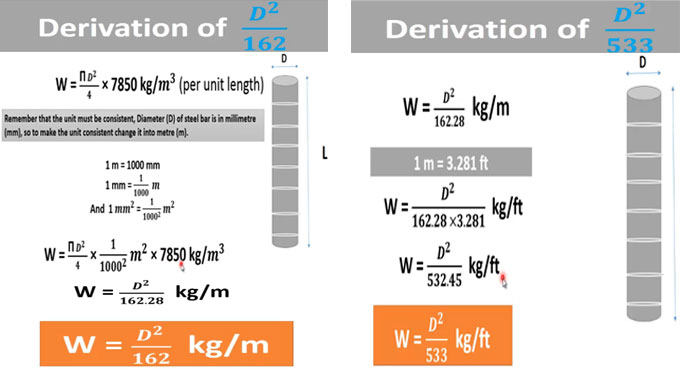
The formula D2/162 is applied when the length is provided in metres and D2/533 is applied when the length of steel bar is provided in feet.
It is known that the weight of steel = volume of steel bar x unit weight of steel
i.e. W = V x ? (? stands for gamma)
Volume (V) = Cross sectional area x Length = A x L
So, W = A x L x ?
The area of circular section is determined with the following formula :-
?d2/4
So, putting the value, we get the following :-
W = ?d2/4 x L x ?
If it is required to determine the weight of steel in kilogram per unit length, the length (L) should be omitted.
So, W = ?d2/4 x ?
It is known as the unit weight of steel (?) in MKS system is 7850 kg/m3
W = ?d2/4 x 7850 kg/m3 (per unit length)
Diameter (D) of steel bar is given into millimeter (mm) and it should be transformed into metre (m) to make the unit uniform.
As we know, 1 m = 1000 mm
1 mm = 1/1000 m
1 mm2 = 1/10002 m2
After putting the above value, we get the following result :-
W = ?d2/4 x 1/10002 m2 x 7850 kg/m3
W = D2/162.28 kg/m
W = D2/162 kg/m
In order to learn how D2/533 is derived, go through the following video tutorial.
Video Source: Civil Engineering World - THE CIVILOIDS