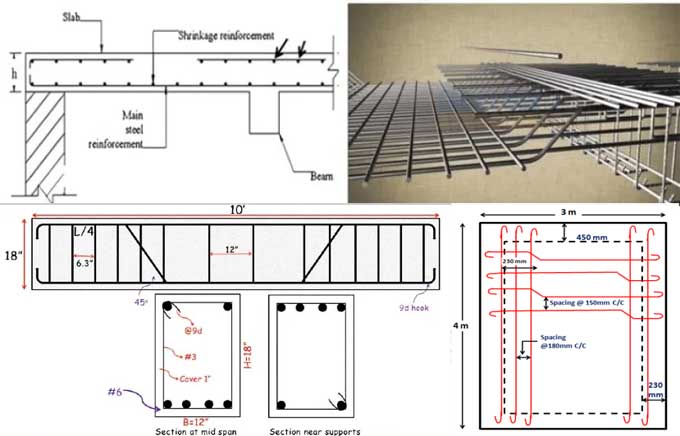
Slab Steel Quality Calculation from Drawing and BBS of Slab
Estimating steel quantities is a key skill for civil engineers. The method of calculating steel quantity from a drawing must be known by all civil engineers.
Steel quantity estimation requires the following data:
- Plan, Section & Elevation.
- Slab & Beam Structural Details.
- Clear & Co-related Dimensions.
Slab BBS Preparation
BBS is calculated as follows:
- Slab.
- Slab Beam.
Slab Bar
How to Cut a Slab Bar to Length
Length of the bent up bars after cutting = (Total length) + ((0.42 x d)) + lap
The area contained within (-1 to 3)/(-A to +B)
Direction X
The tests will not indicate how well the concrete can pass between the reinforcement without blocking, but they may indicate how well it resists segregation.
Dimensions: 8 mm Diameter, 200 mm center-to-center.
The number of bars is (7/0.2) x 1 = 36 nodes, which is the number of bars.
In this case, (0.162 * (0.125-0.025-0.025)) + 0.42 is the cut bar of (0.100+2.400+4.300+1.000+2.800+1.000+0.100) set as cutting bar.
The Cut Bar is equal to (11.700) + (0.032) = 11.732 m.
A slab bar's total weight is determined by the number of bars, the number of cutting lengths, and the total weight of the bars.
Weight of X-direction slab bars = 36 times 11.732 times 0.39.
In Y Direction
Dimensions: 8 mm Diameter, 200 mm center-to-center.
Total Number of Bars = (11.700/0.200)+ 1 = 59.5 Nos. = 60 Nos.
Calculated cutting bar: (0.100+1.800+3.200+1.800+0.100) + (0.42) * (0.125-0.025-0.025) + 0.
Bar Cutting = (7.000) + (0.315) = 7.032 m.
The total weight of a slab bar in the Y direction is equal to the number of bars x the cutting length x the weight of bars.
Weighing 166.658 kg for Y-direction slab bar is 60 x 7.0032 x 0.39.
Additional bars
10mm Diameter 200mm Center to Center
Total Number of Bars = (11.700/0.200)+ 1 = 59.5 Nos. = 60 Nos.
An area of TB2 divided by TB2 area (from -1 to +3) = (1.600m + 0.900m + 0.200m).
TB1 weighs the total number of bars divided by the cutting length multiplied by the diameter of the bar.
TB1 has a mass of 59.136 kg which is the result of 60 times 1.600 times 0.6616.
The number of bars is (7/0.2) x 1 = 36 nodes, which is the number of bars.
TB3 (-A to +B) is equal to (0.700 + 0.200 + 1.250) = 2.150m.
There are 47.678 kg in total weight of TB3.
The number of bars is (7/0.2) + 1 = 36. = 36.0.
Area half of TB5 (-A to +B) = (1.250 + 0.200 + 1.400) = 2.850 m.
The total weight of TB5 is 36 X.
A weight of 63.202 kg is calculated by multiplying 2.850 by 0.6616.
In a slab, the total weight is the weight of the slab bar in the X direction plus the weight of the slab bar in the Y direction.
TB1 + TB3 + TB5 = slab bar + total weights.
A slab weighs 503.03 kg if it consists of 166.829 kg, 166.658 kg, 59.136 kg, 47.678 kg, and 63.202 kg.
Slab Beam
Bar-number of stirrups
The formula below allows us to find the number of stirrups by multiplying the spacing of the stirrups with the length that the stirrups are placed along.
[(14.100-200) / 200)] + 1 = 70.5 No?s
There are 71 stirrups in total
The Stirrup Length to Cut Off
Measurement of beam stirrup length
Hook at 90 degrees:
Measures the length of stirrup by multiplying it by 2 (A + B).
Hook at 135 degrees:
In general, stirrups have a circumference of 24 x diameter (A + B)
Stirrup length = 2 ((Length -2) Cover + 2 (Breadth -2) Cover + 24 x diameter
Stirrup diameter
Measure the stirrups by multiplying (1.50 + 0.550) by 24 x 8
Stirrup length is 1.592 meters.
The total weight of the stirrups
Total Weight Stirrups = (Reinforcement Rings x Cutting Length) x (Weight diameter of bars)
The total weight of the stirrups is (71 x 1.592) x (0.395) = 44.648 kg
The nature of steel is ductile, so its elasticity is subject to elongation. Therefore, bends and hooks increase a bar's length. In order to counteract this lengthening, certain deduction must be made.
Using different lengths of bars
Bars are measured by their cutting length less any deductions
If the angle is 45 degrees
Taking the total length less the diameter divided by the number of bends gives the cutting length Calculate cutting length by multiplying (Total Length) by (2 x L length) and (Lap Length (45 x D)) by (2 x Bend) ? (Cover).
Bottom Bar
Two 16mm diameter bars
The cutting length is (11.1400+2.400+0.200) with (2x 0.550) minus (45x16) minus (2x0.016) minus (2x0.025).
A cutting length equals (14.100) + (1.100) + (0.720) minus (0.032) minus (0.050)
15.838 meters is the cutting length
Bottom bar weight = No. of bars times Cutting length times Weight of bars
Two 15.838 by one 1.580 equals 50.048 grams of bottom bar weight
Top Bar
Two 20 mm diameter bars
To calculate the cutting length, multiply (11,400+2,400+0.200) by ( 2x 0.550) ? ( 45 x 20) - ( 2x 0.020) -(2x 0.025)
The cutting length is equal to (14.100) plus (1.100) plus (0.900) - (0.040) - (0.050)
15.10 m is the length of the cutting
The total weight of a top bar is the number of bars multiplied by the cutting length divided by the weight of the bars
Two 16 10 by two 2 469 kilograms equals 79.057 kilograms of top bar
The total weight of the beam is the sum of the weight of the stirrups, the weight of the bottom bar, and the weight of the top bar
There are 144.648kg of beam weight, 50.048kg of beam weight and 79.057kg of beam weight, so 173.753kg.